Ejercicio 5

Utilizando casillas de control realiza una traslación, un giro, una simetría axial y una simetría central de una figura cualquiera.

Traslación 

Movimiento directo sin cambio de orientación, es decir, manteniendo la forma y el tamaño del objeto que se traslada.  todos los puntos de la figura se mueven en la misma dirección y a la misma distancia. Lo que da como resultado una figura exactamente igual, desplazada a una determinada distancia y en una dirección determinada según el vector. 

Rotación o giro 

Movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura u objeto original. 

En cualquier giro es importante:

- el ángulo que determina la amplitud de rotación.

- el centro de rotación. 

- el sentido de giro, que puede ser el mismo que las agujas del reloj o al contrario.

Simetría axial

Simetría que se produce alrededor de un eje. Es decir, aquella que tiene lugar cuando los semiplanos que se toman a partir de un mencionado eje, al que contienen, presentan idénticas características.

En la simetría axial se produce el mismo fenómeno que se da al reflejar cualquier objeto en un espejo.

A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica.

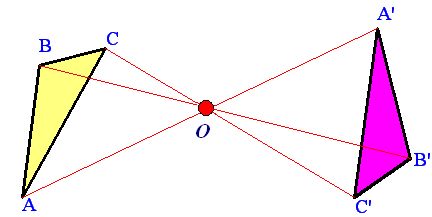
Simetría central

Transformación en la que a cada punto se le asocia otro punto llamado imagen, que debe cumplir las siguientes condiciones:

a) El punto y su imagen están a igual distancia de un punto llamado centro de simetría.                         

b) El punto, su imagen y el centro de simetría pertenecen a una misma recta.

A continuación dejo un vídeo explicando como hacerlo :